March 15, 2022

D^3CTF2022-D3w0w

这场比赛坐大牢，一题一个架构，赛后看看发现出的也不是特别难，赛中学习还是挺重要的，这题本来有机会出的，别人来了句纸笔都能算，直接拉着密码师傅大白兔手推去了，淦！

0x00 日常查壳

无壳32位

image-20220315104143478

0x01 分析主函数

主程序清晰明了，就是通过这两个函数返回的值来判断是否正确

这里是401000函数通过flag初始化了data区域，然后401220拿data去验证，同时通过32位转64做了点混淆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int __cdecl main(int argc, const char **argv, const char **envp)
{
  char input[40]; // [esp+0h] [ebp-30h] BYREF
  BOOL v5; // [esp+28h] [ebp-8h]
  BOOL v6; // [esp+2Ch] [ebp-4h]

  dword_4262F0 = (int)NtCurrentTeb()->WOW32Reserved;
  memset(input, 0, 0x27u);
  sub_402100("%39s", input);
  v6 = sub_401000((int)input, (int)&data) || sub_401220();
  v5 = v6;
  if ( v6 )
    sub_402090("you lose\n", input[0]);
  else
    sub_402090("you win\n", input[0]);
  return 0;
}

0x02 401000函数

这个函数给出了flag的第一位是2，每次迷宫题都没反应出迷宫题…明明这么明显，虽然这题也不完全算迷宫题

这个函数需要注意的是

  1. 每当走一步当前格子和目标格子就都会设置！划重点！

  2. 并且边界也告诉了，也就是<0 和 >5，其实就是6x6的地图

  3. 第一个flag是2，所以data[0] |= 2，data[6] |= 8

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
int __cdecl sub_401000(int a1, int a2)
{
  int v3; // [esp+0h] [ebp-10h]
  int v4; // [esp+8h] [ebp-8h]
  int v5; // [esp+Ch] [ebp-4h]

  v5 = 0;
  v4 = 0;
  v3 = 6;
  if ( *(_DWORD *)a1 != 'tc3d' )
    return 1;
  if ( *(_WORD *)(a1 + 4) != '{f' )
    return 1;
  if ( *(_BYTE *)(a1 + 6) != '2' )
    return 1;
  while ( *(_BYTE *)(v3 + a1) != '}' )
  {
    switch ( *(_BYTE *)(v3 + a1) )              // 每当走一次 当前格子和目标格子都会给设置一个数
    {
      case '1':
        *(_DWORD *)(a2 + 24 * v5 + 4 * v4) |= 8u;// 上
        *(_DWORD *)(a2 + 24 * --v5 + 4 * v4) |= 2u;
        goto LABEL_14;
      case '2':
        *(_DWORD *)(a2 + 24 * v5 + 4 * v4) |= 2u;// 下
        *(_DWORD *)(a2 + 24 * ++v5 + 4 * v4) |= 8u;
        goto LABEL_14;
      case '3':
        *(_DWORD *)(a2 + 24 * v5 + 4 * v4) |= 4u;// 左
        *(_DWORD *)(a2 + 24 * v5 + 4 * v4-- - 4) |= 1u;
        goto LABEL_14;
      case '4':
        *(_DWORD *)(a2 + 24 * v5 + 4 * v4) |= 1u;// 右
        *(_DWORD *)(a2 + 24 * v5 + 4 * v4++ + 4) |= 4u;
LABEL_14:
        if ( v5 < 0 || v4 < 0 || v5 > 5 || v4 > 5 )
          return 1;
        ++v3;
        break;
      default:
        return 1;
    }
  }
  return 0;
}

0x03 401220函数

这个函数是通过222510函数跳到了64位，很明显的push 33 retf的标识

image-20220315105221394

直接去od里dump这个函数

image-20220315110217962

然后直接去010新建一个16进制文件放进去即可

image-20220315110750892

丢进ida64即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
// positive sp value has been detected, the output may be wrong!
__int64 __fastcall sub_0(_DWORD *m)
{
  int v2; // [rsp-8h] [rbp-B0h]
  int v3; // [rsp-8h] [rbp-B0h]
  int row; // [rsp-8h] [rbp-B0h]
  int v5; // [rsp-4h] [rbp-ACh]
  int v6; // [rsp-4h] [rbp-ACh]
  int col; // [rsp-4h] [rbp-ACh]
  int i; // [rsp+0h] [rbp-A8h]
  int j; // [rsp+4h] [rbp-A4h]
  int v10; // [rsp+8h] [rbp-A0h]
  int v11; // [rsp+Ch] [rbp-9Ch]
  int k; // [rsp+10h] [rbp-98h]
  int l; // [rsp+14h] [rbp-94h]
  unsigned int v14; // [rsp+18h] [rbp-90h]
  unsigned int v15; // [rsp+1Ch] [rbp-8Ch]
  unsigned int v16; // [rsp+20h] [rbp-88h]
  unsigned int v17; // [rsp+24h] [rbp-84h]
  unsigned int v18; // [rsp+28h] [rbp-80h]
  unsigned int v19; // [rsp+2Ch] [rbp-7Ch]
  int v20[3]; // [rsp+30h] [rbp-78h]
  int v21[10]; // [rsp+40h] [rbp-68h]
  __int64 v22; // [rsp+68h] [rbp-40h]
  __int64 v23; // [rsp+70h] [rbp-38h]
  __int64 v24; // [rsp+78h] [rbp-30h]
  __int64 v25; // [rsp+80h] [rbp-28h]
  __int64 v26; // [rsp+88h] [rbp-20h]
  __int64 v27; // [rsp+90h] [rbp-18h]

  v20[0] = 0;
  v20[1] = 14;
  v20[2] = 20;
  v21[0] = 4;
  v21[1] = 13;
  v21[2] = 15;
  v21[3] = 21;
  v21[4] = 24;
  v21[5] = 31;
  v21[6] = 32;
  v21[7] = 41;
  v21[8] = 45;
  v21[9] = 53;
  for ( i = 0; i < 6; ++i )                     // 总体限制 所以这里的总体限制就是每个各自只能走一次
  {
    for ( j = 0; j < 6; ++j )
    {
      if ( m[6 * i + j] > 0xFu )                // 长度为36 且都小于等于15 每个值的可能性是1 2 4 8
        return MEMORY[0x12F5]();
      v14 = m[6 * i + j] % 0x10u / 8;
      v22 = j;
      v15 = m[6 * i + j] % 8u / 4 + v14;
      v23 = j;
      v16 = m[6 * i + j] % 4u / 2 + v15;
      v24 = j;
      if ( m[6 * i + j] % 2u + v16 > 2 || !j && m[6 * i] % 8u / 4 )// j == 0, a[6 * i] = 4
        return MEMORY[0x12F5]();
      if ( j == 5 && m[6 * i + 5] % 2u || !i && m[j] % 0x10u / 8 || i == 5 && m[j + 30] % 4u / 2 )
        return MEMORY[0x12F5]();
    }
  }

  for ( k = 0; (unsigned __int64)k < 3; ++k )   // 于是可以判断这三个点 必须拐弯
  {
    v2 = v20[k] / 10;
    v5 = v20[k] % 10;                           // （0，0）（1，4）（2，0）
    if ( m[6 * v2 + v5] % 0x10u / 8 && m[6 * v2 + v5] % 4u / 2 )
      return MEMORY[0x12F5]();
    if ( m[6 * v2 + v5] % 8u / 4 && m[6 * v2 + v5] % 2u )
      return MEMORY[0x12F5]();
    v17 = m[6 * v2 + v5] % 0x10u / 8;
    v25 = v5;
    v18 = m[6 * v2 + v5] % 4u / 2 + v17;
    v26 = v5;
    v19 = m[6 * v2 + v5] % 2u + v18;
    v27 = v5;
    if ( m[6 * v2 + v5] % 8u / 4 + v19 != 2 )
      return MEMORY[0x12F5]();
    if ( m[6 * v2 + v5] % 0x10u / 8 )           // 当前位置记录了“上” 上一行不能也是“上”
    {
      if ( !(m[6 * v2 - 6 + v5] % 0x10u / 8) )
        return MEMORY[0x12F5]();
    }
    else if ( m[6 * v2 + v5] % 4u / 2 )         // 其他同理
    {
      if ( !(m[6 * v2 + 6 + v5] % 4u / 2) )
        return MEMORY[0x12F5]();
    }
    else if ( m[6 * v2 + v5] % 8u / 4 )
    {
      if ( !(m[6 * v2 - 1 + v5] % 8u / 4) )
        return MEMORY[0x12F5]();
    }
    else if ( m[6 * v2 + v5] % 2u && !(m[6 * v2 + 1 + v5] % 2u) )
    {
      return MEMORY[0x12F5]();
    }
  }
  for ( l = 0; (unsigned __int64)l < 0xA; ++l )
  {
    v3 = v21[l] / 10;                           // (0,4) (1,3)
    v6 = v21[l] % 10;
    if ( (!(m[6 * v3 + v6] % 0x10u / 8) || !(m[6 * v3 + v6] % 4u / 2))// 只能是上下走 或者 左右走
      && (!(m[6 * v3 + v6] % 8u / 4) || !(m[6 * v3 + v6] % 2u))

      || m[6 * v3 + v6] % 0x10u / 8             // 用来判断是上下的
                                                // 只要下一行或上一行有个拐弯 也就是左右走
      && m[6 * v3 + v6] % 4u / 2
      && !(m[6 * v3 - 6 + v6] % 8u / 4)
      && !(m[6 * v3 - 6 + v6] % 2u)
      && !(m[6 * v3 + 6 + v6] % 8u / 4)
      && !(m[6 * v3 + 6 + v6] % 2u)

      || m[6 * v3 + v6] % 8u / 4                // 用来判断左右的
                                                // 只要上格子或下个各自有一个上下拐外即可
      && m[6 * v3 + v6] % 2u
      && !(m[6 * v3 + 1 + v6] % 0x10u / 8)
      && !(m[6 * v3 + 1 + v6] % 4u / 2)
      && !(m[6 * v3 - 1 + v6] % 0x10u / 8)
      && !(m[6 * v3 - 1 + v6] % 4u / 2) )
    {
      return MEMORY[0x12F5]();
    }
  }
  v10 = 0;
  v11 = 0;
  row = 0;
  col = 0;
  if ( *m % 0x10u / 8 )
  {
    row = -1;
    while ( 1 )
    {
LABEL_67:
      if ( !(m[6 * row + col] % 0x10u / 8) || row - 1 == v10 && col == v11 )
      {
        if ( !(m[6 * row + col] % 4u / 2) || row + 1 == v10 && col == v11 )
        {
          if ( !(m[6 * row + col] % 8u / 4) || row == v10 && col - 1 == v11 )
          {
            if ( !(m[6 * row + col] % 2u) || row == v10 && col + 1 == v11 )
              return MEMORY[0x12F5]();
            v10 = row;
            v11 = col++;
          }
          else
          {
            v10 = row;
            v11 = col--;
          }
        }
        else
        {
          v10 = row;
          v11 = col;
          ++row;
        }
      }
      else
      {
        v10 = row;
        v11 = col;
        --row;
      }
      if ( !row && !col )
        return MEMORY[0x12F5]();
    }
  }
  if ( *m % 4u / 2 )
  {
    row = 1;
    goto LABEL_67;
  }
  if ( *m % 8u / 4 )
  {
    col = -1;
    goto LABEL_67;
  }
  if ( *m % 2u )
  {
    col = 1;
    goto LABEL_67;
  }
  return MEMORY[0x12F5]();
}

0x05 GetFlag!

执笔解法

通过官方WP得知这是masyu

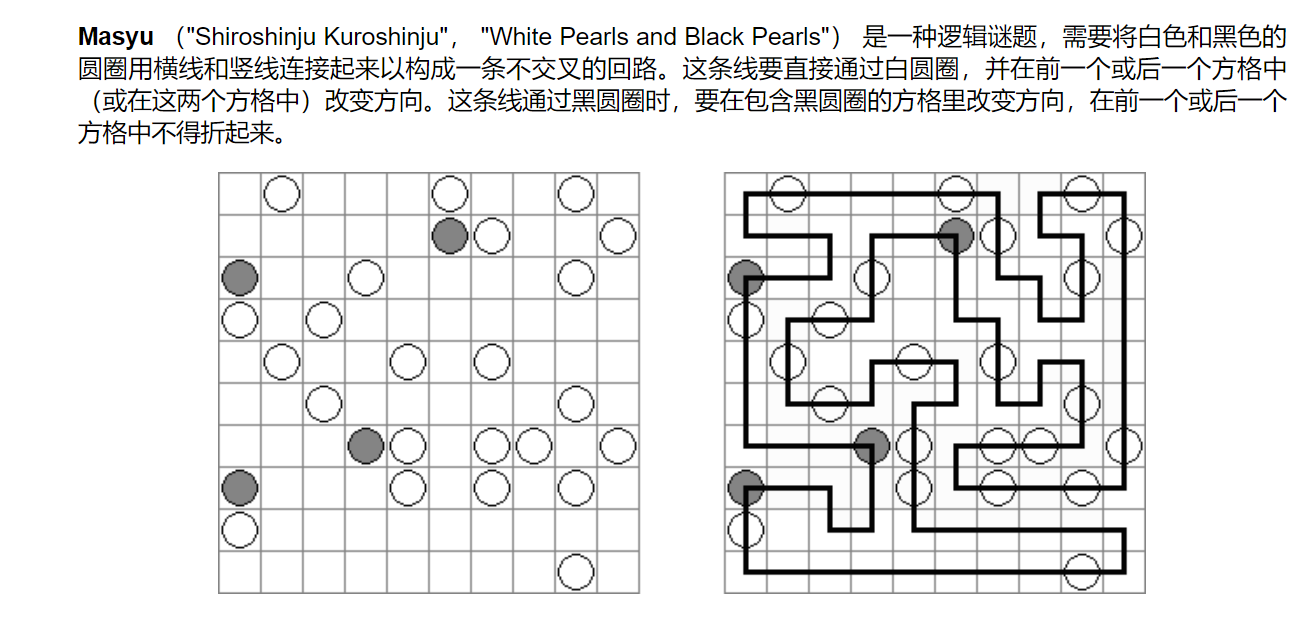
image-20220315111730518

可以上这个网站玩玩

image-20220315111706732

于是通过分析 401220 函数可以得知白点和黑点，真执笔都能算

GetFlag!

image-20220315111855068

Z3解法

打比赛时想到的解法，多半是作者的非预期了，不过没看出来那些特殊点的人应该都靠Z3解了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
from z3 import *

res = [0, 14, 20, 0, 4, 13, 15, 21, 24, 31, 32, 41, 45, 53]
m = [BitVec('%i' % i, 32) for i in range(36)]
# 多加一组因为会溢出计算 数据最后不取即可
m += [0, 0, 0, 0, 0, 0, 0]
sol = Solver()

for i in range(6):
    for j in range(6):
        sol.add(m[6 * i + j] < 0x10)
        sol.add(m[6 * i + j] >= 0)
        # 这个约束很重要！！如果不加就是有一堆数据，这个约束是判断1 2 4 8的个数，在已知<=2的可能性下，
        # 还得知每次走格子必会影响当前和下个，也就是说每个格子要么是走了于是必为记录两次，要么是0次，去掉可能性是1次，即可得到正确数据
        sol.add(((m[6 * i + j] & 0xF) >> 3) + ((m[6 * i + j] & 0x7) >> 2) + ((m[6 * i + j] & 0x3) >> 1) + (m[6 * i + j] & 0x1) & 1 == 0)
        sol.add(((m[6 * i + j] & 0xF) >> 3) + ((m[6 * i + j] & 0x7) >> 2) + ((m[6 * i + j] & 0x3) >> 1) + (m[6 * i + j] & 0x1) <= 2)
        if j == 0:
            sol.add((m[6 * i + j] & 7) >> 2 == 0)
        if j == 5:
            sol.add((m[6 * i + j] & 1) == 0)
        if i == 0:
            sol.add((m[j] & 0xf) >> 3 == 0)
        if i == 5:
            sol.add((m[j + 30] & 3) >> 1 == 0)

for q in range(3):
    v2 = res[q] // 10
    v5 = res[v2] % 10
    # 解锁新方法
    sol.add(
        Or(
            (m[6 * v2 + v5] & 0xF) >> 3 == 0, (m[6 * v2 + v5] & 0x3) >> 1 == 0
        )
    )
    sol.add(
        Or(
            (m[6 * v2 + v5] & 0x7) >> 2 == 0, (m[6 * v2 + v5] & 0x1) == 0
        )
    )
    sol.add(((m[6 * v2 + v5] & 0xF) >> 3) + ((m[6 * v2 + v5] & 0x7) >> 2) + ((m[6 * v2 + v5] & 0x3) >> 1) + (m[6 * v2 + v5] & 0x1) == 2)
    sol.add(
        Or(
            (m[6 * v2 + v5] & 0xF) >> 3 == 0, (m[6 * v2 - 6 + v5] & 0xF) >> 3 != 0
        )
    )
    sol.add(
        Or(
            (m[6 * v2 + v5] & 0x3) >> 1 == 0, (m[6 * v2 + 6 + v5] & 0x3) >> 1 != 0
        )
    )
    sol.add(
        Or(
            (m[6 * v2 + v5] & 0x7) >> 2 == 0, (m[6 * v2 - 1 + v5] & 0x7) >> 2 != 0
        )
    )
    sol.add(
        Or(
            (m[6 * v2 + v5] & 0x1) == 0, (m[6 * v2 + 1 + v5] & 0x1) != 0
        )
    )
for q in range(10):
    v3 = res[q + 4] // 10
    v6 = res[q + 4] % 10
    sol.add(
        Or(
            And((m[6 * v3 + v6] & 0xF) >> 3 != 0, (m[6 * v3 + v6] & 0x3) >> 1 != 0),
            And((m[6 * v3 + v6] & 0x7) >> 2 != 0, (m[6 * v3 + v6] & 0x1) != 0)
        )
    )
    sol.add(
        Or(
            (m[6 * v3 + v6] & 0xF) >> 3 == 0,
            (m[6 * v3 + v6] & 0x3) >> 1 == 0,
            (m[6 * v3 - 6 + v6] & 0x7) >> 2 != 0,
            (m[6 * v3 - 6 + v6] & 0x1) != 0,
            (m[6 * v3 + 6 + v6] & 0x7) >> 2 != 0,
            (m[6 * v3 + 6 + v6] & 0x1) != 0,
        )
    )
    sol.add(
        Or(
            (m[6 * v3 + v6] & 0x7) >> 2 == 0,
            (m[6 * v3 + v6] & 0x1) == 0,
            (m[6 * v3 + 1 + v6] & 0xF) >> 3 != 0,
            (m[6 * v3 + 1 + v6] & 0x3) >> 1 != 0,
            (m[6 * v3 - 1 + v6] & 0xF) >> 3 != 0,
            (m[6 * v3 - 1 + v6] & 0x3) >> 1 != 0,
        )
    )

sol.add((m[0] & 0x3) >> 1 == 1)

for i in range(6):
    for j in range(6):
        # 这边是做了个自己理解的约束
        # 拿一条举例 前一个是右移 当右移后右边的格子必会或上4 所以两边经过取余+右移的计算都会有个1
        # 于是每一条都这样加上限制就可以拿到最后的数据
        sol.add((m[6 * i + j] & 0x1) == (m[6 * i + (j + 1)] & 0x7) >> 2)
        sol.add((m[6 * i + j] & 0x3) >> 1 == (m[6 * (i + 1) + j] & 0xf) >> 3)
        sol.add((m[6 * i + j] & 0x7) >> 2 == (m[6 * i + (j - 1)] & 1))
        sol.add((m[6 * i + j] & 0xf) >> 3 == (m[6 * (i - 1) + j] & 0x3) >> 1)

# 这种方法可以跑出所有数据
# 写这个脚本的师傅应该就是不断看跑出来的数据再去加上限制 学习到了
while sol.check() == sat:
    s = sol.model()
    print([s[i].as_long() for i in m[:36]])
    # 这条总体来说是让以后的解不等于现在的解
    # s[m[i]]是现在的解 m[i]是z3的 于是就是在增加条件
    # 同时用上Or 这样只要有一位不相等 就是两组不同的解 继而跑其他可能
    # 感谢v0id师傅一语点破
    sol.add(Or([m[i] != s[m[i]] for i in range(36)]))

flag = ''
data = [3, 5, 5, 5, 5, 6, 10, 0, 3, 5, 6, 10, 9, 5, 12, 0, 10, 10, 3, 5, 5, 6, 10, 10, 9, 5, 6, 9, 12, 10, 0, 0, 9, 5, 5, 12]
map = [0] * 36
map[0] = 2
map[6] = 8
x = 1
y = 0
while ( map[0] != 3 ):
    for i in range(1, 5):
        if i == 1 and x - 1 >= 0:
            if map[x * 6 + y] + 8 == data[x * 6 + y]:
                map[x * 6 + y] |= 8
                map[(x - 1) * 6 + y] |= 2
                x -= 1
                flag += str(i)
                break
        if i == 2 and x + 1 <= 5:
            if map[x * 6 + y] + 2 == data[x * 6 + y]:
                map[x * 6 + y] |= 2
                map[(x + 1) * 6 + y] |= 8
                x += 1
                flag += str(i)
                break
        if i == 3 and y - 1 >= 0:
            if map[x * 6 + y] + 4 == data[x * 6 + y]:
                map[x * 6 + y] |= 4
                map[x * 6 + y - 1] |= 1
                y -= 1
                flag += str(i)
                break
        if i == 4 and  y + 1 <= 5:
            if map[x * 6 + y] + 1 == data[x * 6 + y]:
                map[x * 6 + y] |= 1
                map[x * 6 + y + 1] |= 4
                y += 1
                flag += str(i)
                break
print("d3ctf{" + flag + "}")

GetFlag!

image-20220315112058210

DASCTF X SU
🍬
HFCTF2022
🍪

About this Post

This post is written by P.Z, licensed under CC BY-NC 4.0.